斐波那契数列的几种写法

发表于 | 分类于 |

斐波那契数列

斐波那契数列（意大利语：Successione di Fibonacci），又译为费波拿契数列、费波那西数列、斐波那契数列、黄金分割数列。

在数学上，费波那契数列是以递归的方法来定义：

F[0] = 0 
F[1] = 1 
F[n] = F[n − 1] + F[n − 2] （n≧2）

用文字来说，就是费波那契数列由0和1开始，之后的费波那契系数就是由之前的两数相加而得出。首几个费波那契系数是：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……

特别指出：0不是第一项，而是第零项。

好了，以上的摘自wiki，现在我就用python写一下求取数列第n项的方法：

  • 按数学定义的递归方法：
1
2
3
4
5
6
7
8

def fibd(n):#递归的写法
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibd(n-1)+fibd(n-2)

可以把参数n看成是问题的规模，不难看出，计算F[n]的时间代价（考虑求假发操作的次数）大致等于F[n-1]和F[n-2]的时间代价之和，也可以基本时间代价是指数增长的。而且每次调用一个函数的时候，系统都会重新开辟一个与这个函数相对应的栈帧。如果递归调用的深度比较大，栈帧会开辟很多，一来是浪费空间，二来性能也必然会下降很多（有很多读写内存操作）。

所以有没有什么可以优化的地方呢？可以比较明显看出，其实每次计算的时候有很多重复计算，所以如果我们可以将已经计算的参数记录下来，以供后面使用，这样就会节省部分时间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from functools import wraps
def memo(func):
    cache={}
    @wraps(func)
    def wrapper(n):
        if n not in cache:
            cache[n]= func(n)
        return cache[n]
    return wrapper

@memo
def fibd(n):
    if n == 0:
        return 0
    elif n ==1:
        return 1
    else:
        return fibd(n-1)+fibd(n-2)

这里再展开说一下关于装饰器调用递归函数，这里的用法直接调用就可以了，如果是下面计算时间的，就必须要再封装一次，而上面的装饰器是不需要的，你明白为什么要这样么？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def calc_time(func):
    def swrapper(*args, **kwargs):
        ti1 = time.time()
        x = func(*args, **kwargs)
        ti2 = time.time()
        print(func.__name__,"time cost",":",ti2-ti1)
        return x
    return swrapper
@calc_time
def fibd(n):
    return _fibd(n)
def _fibd(n):
    if n == 0: return 0
    elif n ==1: return 1
    else: return _fibd(n-1) + _fibd(n-2)
  • 循环迭代

由于我们看到，后一项是前两项的叠加，所以我们可以考虑用循环实现。

1
2
3
4
5
6

def fibf(n): #循环迭代的写法
    cur,nex = 0,1
    for _ in range(n):
        cur,nex = nex,cur+nex
    return cur

明显看出，使用循环，只在一个函数栈空间里，不会开辟更多的空间，所以使用循环，性能要远远好于递归。

  • 矩阵运算

对于F[n] = F[n − 1] + F[n − 2] （n≧2）这样的递推公式，我们可以考虑构建一个二维的递归公式：

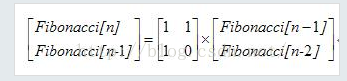
20161004200323252

可以写出一直递推到F[1]，F[0]的公式，前面是矩阵的次幂形式：

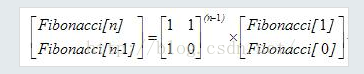
20161004200246626

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

def fibmat(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        k = mat([[1, 1], [1, 0]])
        tmp = powmat(k,n-1)
        res = dot(tmp, mat([[1], [0]]))
        return int(res[0][0])

def powmat(mat,n):
    if n ==0:
        return 1
    elif n % 2 == 0:
        tmp = powmat(mat,n/2)
        return dot(tmp, tmp)
    else:
        return dot(mat, powmat(mat,n-1))
  • 尾递归形式

这个是从知乎上学到的知识点，链接 https://zhuanlan.zhihu.com/p/24305359

1
2
3
4
5
6

def fibw(a,b,n):#尾递归的写法
    if n == 0:
        return a
    else:
        return fibw(b,a+b,n-1)

循坏改成尾递归的通用技巧，那就是把循环的写法中，需要使用变量的地方，都改成递归参数。

几种写法写完了，可以拿去测一下时间了，看看哪个快一些呢。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#2**32=4294967296
46th：
fibd  's result:1836311903;cost time:0.0
fibf  's result:1836311903;cost time:0.0
fibw  's result:1836311903;cost time:0.0
fibmat's result:1836311903;cost time:0.0
47th：
fibd  's result:2971215073;cost time:0.0
fibf  's result:2971215073;cost time:0.0
fibw  's result:2971215073;cost time:0.0
fibmat's result:-1323752223;cost time:0.0  #从47个开始发生了溢出，按位与0xFFFFFFFF为2971215073
100th
fibd  's result:354224848179261915075;cost time:0.0010004043579101562
fibf  's result:354224848179261915075;cost time:0.0
fibw  's result:354224848179261915075;cost time:0.0
fibmat's result:-980107325;cost time:0.0